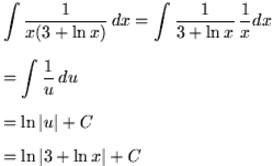Example 1: Solve integral of exponential function ∫e^x32x³dx

Solution: 

Step 1: the given function is ∫e^x^³3x²dx

Step 2: Let u = x³ and du = 3x²dx

Step 3: Now we have: ∫e^x^³3x²dx= ∫e^udu

Step 4: According to the properties listed above: ∫e^xdx = e^x+c, therefore ∫e^udu = e^u + c

Step 5: Since u = x³ we now have ∫e^udu = ∫e^x3dx = e^x^³ + c

So the answer is e^x^³ + c

Example 2:  Integrate .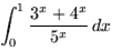

Solution: First, split the function into two parts, so that we get:

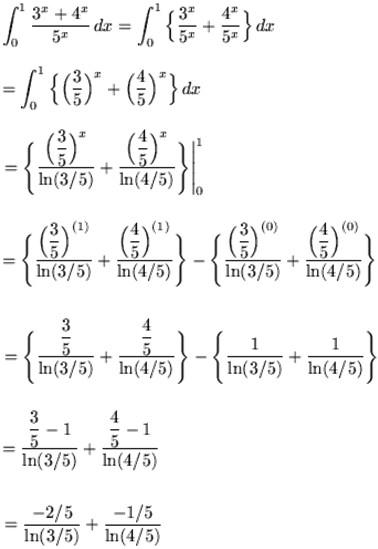
Example 3: Integrate ∫lnx dx.

Solution: 

Let

u=lnu

and

dv = dx = (1)dx

so that:

du = 1/x dx

and

v = x

Therefore:

    ∫lnx dx   

= x lnx - ∫x * 1/x dx  

=xlnx - ∫1dx  

=xlnx – x + C

Example 4: Integrate .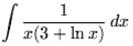

Solution:

Use u-substitution. Let u = 3 + lnx

So that du = 1/x dx.

Substitute into the original problem we will get: