|
ax
|
ax ∙ lna, where a is a constant
|
|
ex
|
ex
|
|
ec∙x
|
c∙ec∙x, where c is a constant
|
|
xx
|
xx(1+ln(x))
|
|
log(x), where the base is 10
|
1/(x∙ln(10))
|
|
loga(x), where the base is a
|
1/(x∙ln(a))
|
|
ln(x)
|
1/x
|
|
f g, f and g are both functions
|
f g(g '∙ln(f)+(g/f)∙f ')
|
Example 1: Find the derivative of f(x) = ln(tan x).
f´(x) = 1 / tan(x) * d/dx * tan(x)
f´(x) = 1 / tan(x) * sec2(x)
Example 2: Find the derivative of f(x) = e(2x-1)
f´(x) = e(2x-1) * d(2x -1 ) / dx
f´(x) = e(2x-1) * 2
Example 3: Find d(3x) / dx
d(3x) / dx = 3xln3
Example 4: Find the derivative of xx-2
Let y =xx-2
Take natural logarithm on both the sides
lny = (x-2)lnx
We now differentiate both sides with respect to x, using chain rule on the left side and the product rule on the right.
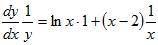
Multiply y on the right hand side
dy/dx = y [lnx*1 + (x-2)/x]
dy/dx = xx-2[lnx*1 + (x-2)/x]
dy/dx =xx-3(x*lnx + x – 2)