Properties of Matrix Operations
Given that Amn, Bmn and Cmn are matrices with m rows and n columns. If c and d are scalars, then the following properties are true.
(cd)A = c(dA)
Commutative property of addition
A + B = B + A
Associative property of addition
A + (B + C) = (A + B) + C
Distributive property
c(A + B) = cA + cB
(c + d)A = cA + dA
Here are some general rules about the three operations: addition, multiplication, and multiplication with numbers, called scalar multiplication.
Properties involving Addition:
Let A, B and C be m×n matrices. We have
1. A+B = B+A
2. (A+B) + C = A + (B+C)
3. A+O = A, where O is the m×n zero-matrix (all its entries are equal to 0).
4. A + B = O, if and only if B = -A.
Properties involving Multiplication:
1. Let A, B and C be three matrices. If the products of AB, (AB) C, BC, and A (BC) are valid, then we have: (AB)C = A (BC)
2. If α and β are numbers, and A is a matrix, then we have:
α (βA) = (α β)A
3. If α is a number, and A and B are two matrices such that the product AB is valid, then we have
α (AB) = (αA)B = A(αB)
4. If A is an n×m matrix and O is a m×k zero-matrix, then we have:
AO = O
Note that AO is the n×k zero-matrix. So if n is different from m, the two zero-matrices are different.
Properties involving Addition and Multiplication:
Let A, B and C be three matrices. If the products of AB, BC and AC are valid, then we have:
(A+B)C = AC + BC
and
A(B+C) = AB + AC
If α and β are numbers, A and B are matrices, then we have:
α (A+B) = αA + βB
and
(α +β) A = αA + βA
Example 1: Calculate 4C, AD, DA, BC, 3CB, C (A + B), AB, BA, CAD, DBC, AD + (CB)T, DC and CD for the given matrices below.
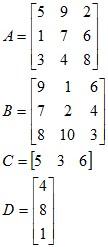
Solution:
4C = [20 12 24]
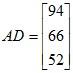
DA - The dimensions are not valid for multiplication (3 by 1 multiplied by 3 by 3). The inside dimensions do not agree.
BC - The dimensions are not valid for multiplication (3 by 3 multiplied by 1 by 3). The inside dimensions do not agree.
3CB = [342 213 180]
C (A + B) = [ 160 161 136 ]
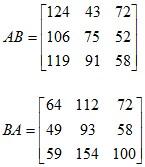
CAD = 980
DBC - The dimensions are not valid for multiplication (3 by 1 × 3 by 3 × 1 by 3). The inside dimensions do not agree on either multiplication.
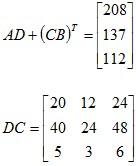
CD = 50
Example 2: What matrix would need to be added to A to produce the 3 by 5 zero matrix if

Solution:
The required matrix can be given as
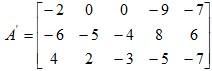
Example 3: Given that:
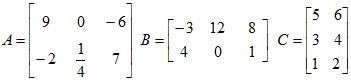
Calculate:
A + B
A – B
C + A
Solution:
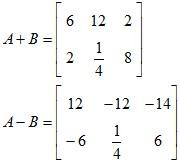
C + A: Not possible to calculate as both the matrices are of different dimension.