Definition of an Inverse of a Matrix
Assuming that we have a square matrix A, which is non-singular (i.e. det (A) does not equal zero), then there exists an n × n matrix A-1 which is called the inverse of A such that:
AA-1 = A-1A = I, where I is the identity matrix.
The inverse of a 2×2 matrix
Take for example an arbitrary 2×2 Matrix A whose determinant (ad − bc) is not equal to zero.
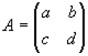
where a, b, c and d are numbers.
The inverse is:
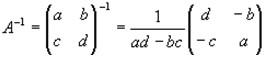
The inverse of a general n × n matrix A can be found by using the following equation.
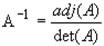
where the adj (A) denotes the adjoint of a matrix. It can be calculated by the following method:
Given the n × n matrix A, define B = bij to be the matrix whose coefficients are found by taking the determinant of the (n-1) × (n-1) matrix obtained by deleting the ith row and jth column of A.
The terms of B (i.e. B = bij) are known as the cofactors of A.
Define the matrix C, where cij = (−1)i+j bij.
The transpose of C (i.e. CT) is called the adjoint of matrix A.
Example 1: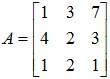 
. Find the adj A.
Solution:
Computation of adj A:
Cofactor of 1 = a11 = - 4
Cofactor of 3 = a12 = -1
Cofactor of 7 = a13 = 6
Cofactor of 4 = a21 = 11
Cofactor of 2 = a22 = -6
Cofactor of 3 = a23 = 1
Cofactor of 1 = a31 = -5
Cofactor of 2 = a32 =-25
Cofactor of 1 = a33 = -10
Therefore we have:
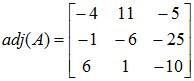
Example 2: Find the inverse of
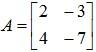
Solution:
The following method to find the inverse is only applicable for 2 × 2 matrices.
1. Interchange leading diagonal elements:
-7 → 2; 2 → -7
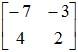
2. Change signs of the other 2 elements:
-3 → 3; 4 → -4
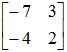
3. Find the determinant |A|
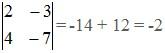
4. Multiply result of [2] by 1/ |A|
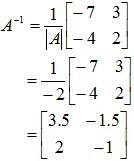
Example 3: Find the inverse of
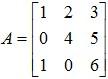
Solution:
The cofactor matrix for A can be calculated as follows:
Cofactor of 1 = a11 = 24
Cofactor of 2 = a12 = 5
Cofactor of 3 = a13 = -4
Cofactor of 0 = a21 = -12
Cofactor of 4 = a22 = 3
Cofactor of 5 = a23 = 2
Cofactor of 1 = a31 = -2
Cofactor of 0 = a32 = -5
Cofactor of 6 = a33 = 4
So the cofactor of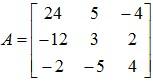 
Therefore, the adjoint of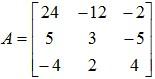 
.
And finally, the inverse of A is given by,
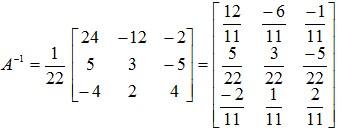
Example 4: Compute the inverse of
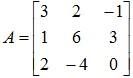
Solution: The cofactor matrix for A can be calculated as follows:
Cofactor of 3: a11 = 12
Cofactor of 2: a12 = 6
Cofactor of -1: a13 = -16
Cofactor of 1: a21 = 4
Cofactor of 6: a22 = 2
Cofactor of 3: a23 = 16
Cofactor of 2: a31 = 12
Cofactor of -4: a32 = -10
Cofactor of 0: a33 = 16
So the cofactor of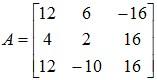 
Therefore the adjoint of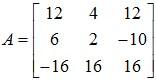 
.
And finally, the inverse of A is given by:
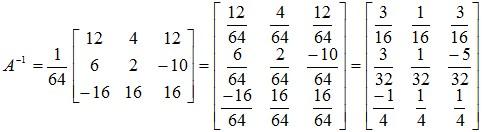
Example 5: Find the inverse of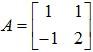 
Solution: Write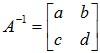 
Since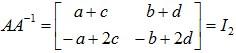 
We have:
a + c = 1
-a + 2c = 0
b + d = 0
-b + 2d = 1
or
a = 2/3
b= -1/3
c=1/3
d= 1/3
The inverse of A is therefore:
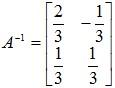
We know that the inverse matrix is unique when it exists. So if A is invertible, then A-1 is also invertible and (A-1)-1 = A.